以下是晶体衍射相关的复习内容
晶体衍射的基本知识
晶体的特点是其内部原子的周期性排列,形成不同方向等间隔的晶面族,每组晶面族可作为波的衍射光栅,通过选择适当波长的波入射到晶体上可观察到晶体衍射现象,晶体衍射实际上是一种基于波叠加原理的干涉现象
若将周期性排布的原子或原子面视为波的衍射光栅,要观察到衍射现象,基本的判据是,所选择波的波长应同晶体中原子间的间距或原子面之间的面间距相当,否则,不可能观察到衍射现象,而只能观察到通常的光的折射现象
各种射线源的特点:
- X射线:可以确定晶体结构但不能研究晶体的表面结构;
- 电子:研究晶体的表面结构;
- 中子:探测晶体的磁有序结构。
晶体衍射的不同表述
劳厄晶体衍射方程
假设一个波长为$\lambda$,沿单位矢量$\vec{S_0}$传播的波,由于晶体的散射,形成了沿单位矢量$\vec{S}$传播的波,则有:
\[\vec R_l\cdot\left(\vec S-\vec S_0\right)=n\lambda\]在倒格子空间中,$\vec{k}=\frac{2\pi}{\lambda}\vec{S}$可以表述为:
\[\vec{R}_l\cdot(\vec{k}-\vec{k}_0)=2\pi n\] \[\vec k-\vec k_0=n\vec K_{h_1h_2h_3}\]$n$称为衍射级数,$(h_1h_2h_3)$称为与发生相长干涉有关的晶面的面指数
布拉格衍射方程
考虑面指数为$(h_1h_2h_3)$的晶面,其面间距为$d_{h_1h_2h_3}$,
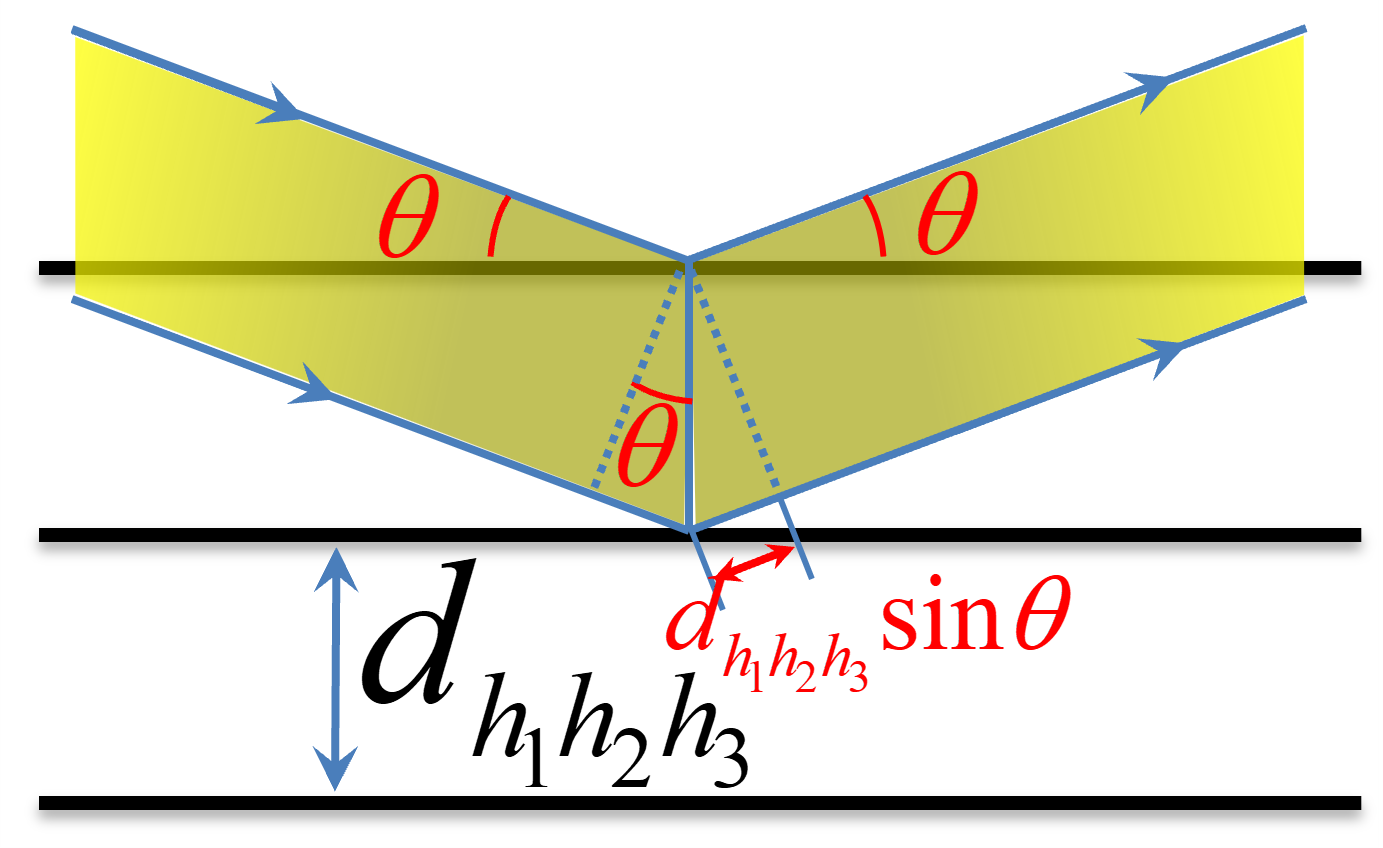
则有:
\[2d_{h_1h_2h_3}\sin\theta=n\lambda\] \[\vec{k}-\vec{k_0}=n\vec{K_h}\]布里渊衍射方程
令$\vec{G}=n\vec{K_h}$,则有$\vec{k_0}=\vec{k}-\vec{G}$,由$k_0^2=k^2$,则
\[2\vec{k}\cdot\vec{G}=\vec{G}^2\]由此得到一个重要的结论,即:当入射波到达布里渊区边界时会产生反射,反射波和入射波相互干涉,导致衍射加强。