以下是固体物理第三章的复习内容
倒格子
构建空间需要一组完备的基矢,而三维实空间下的基矢可以通过傅里叶变换转换到状态空间,
\[(x,y,z)\xrightarrow{F-transform}(\vec{k}_x,\vec{k}_y,\vec{k}_z)\]对于正格子空间下的基矢$\vec{a_1},\vec{a_2},\vec{a_3}$有
\[\begin{cases}\vec{b}_1=\frac{2\pi}{\Omega} (\vec{a}_2\times\vec{a}_3)\\\vec{b}_2=\frac{2\pi}{\Omega} (\vec{a}_3\times\vec{a}_1)\\\vec{b}_3=\frac{2\pi}{\Omega} (\vec{a}_1\times\vec{a}_2)\end{cases}\]则倒格矢为:
\[\vec{K}=h_1\vec{b}_1+h_2\vec{b}_2+h_3\vec{b}_3\]对于正格矢和倒格矢,有:$\vec{a_i}\cdot\vec{b_j}=2\pi\delta_{ij}$
倒格点在倒格子空间完全呈周期排列,每个倒格点周围情况相同,因此,倒格子也可认为是倒易空间的布喇菲格子。每种晶体结构都有两套格子与之相联系:正格子和倒格子,意味着倒格子是与真实空间相联系的傅里叶空间中的晶格
正格矢和倒格矢的关系:
\[\vec{R}_l\cdot\vec{K}_h=(l_1\vec{a}_1+l_2\vec{a}_2+l_3\vec{a}_3)\cdot\left(h_1\vec{b}_1+h_2\vec{b}_2+h_3\vec{b}_3\right)=2\pi\left(l_1h_1+l_2h_2+l_3h_3\right)=2\pi n\]正格子体积和倒格子体积的关系:
\[\Omega^*=\vec{b}_1\cdot\vec{b}_2\times\vec{b}_3=\frac{(2\pi)^3}{\Omega^3}\left(\vec{a}_2\times\vec{a}_3\right)\cdot(\vec{a}_3\times\vec{a}_1)\times(\vec{a}_1\times\vec{a}_2)=\frac{(2\pi)^3}{\Omega}\]一些晶体的倒格子
体心立方晶体:
\[\begin{cases}\vec{a}_1=\frac a2\left(-\vec{i}+\vec{j}+\vec{k}\right)\\\vec{a}_2=\frac a2\left(\vec{i}-\vec{j}+\vec{k}\right)\\\vec{a}_3=\frac a2\left(\vec{i}+\vec{j}-\vec{k}\right)\end{cases}\quad\Rightarrow\quad\begin{cases}\vec{b}_1=\frac{2\pi}a\left(\vec{j}+\vec{k}\right)\\\vec{b}_2=\frac{2\pi}a\left(\vec{i}+\vec{k}\right)\\\vec{b}_3=\frac{2\pi}a\left(\vec{i}+\vec{j}\right)\end{cases}\]面心立方晶体
\[\begin{cases}\vec{a}_1=\frac a2\left(\vec{j}+\vec{k}\right)\\\vec{a}_2=\frac a2\left(\vec{i}+\vec{k}\right)\\\vec{a}_3=\frac a2\left(\vec{i}+\vec{j}\right)\end{cases}\quad\Rightarrow\quad\begin{cases}\vec{b}_1=\frac{2\pi}a\left(-\vec{i}+\vec{j}+\vec{k}\right)\\\vec{b}_2=\frac{2\pi}a\left(\vec{i}-\vec{j}+\vec{k}\right)\\\vec{b}_3=\frac{2\pi}a\left(\vec{i}+\vec{j}-\vec{k}\right)\end{cases}\]由上可知,体心立方和面心立方互为正、倒格子
二维正交结构
\[\begin{aligned}&\overline{b}_{1}=\frac{2\pi}{\left|\vec{a}_{1}\times\vec{a}_{2}\right|}\vec{a}_{2}\times\vec{e}_{3}=\frac{2\pi}{ab}(b\vec{j}\times\vec{k})=\frac{2\pi}{a}\vec{i}\\&\vec{b}_{2}=\frac{2\pi}{\left|\vec{a}_{1}\times\vec{a}_{2}\right|}\vec{e}_{3}\times\vec{a}_{1}=\frac{2\pi}{ab}(\vec{k}\times a\vec{i})=\frac{2\pi}{b}\vec{j}\\&\vec{b}_{3}=\frac{2\pi}{\left|\vec{a}_{1}\times\vec{a}_{2}\right|}\vec{a}_{1}\times\vec{a}_{2}=2\pi\vec{k}\end{aligned}\]倒格子空间中仍为二维正交结构
倒格子与晶面指数、晶向指数的关系
设晶面指数为$(h_1h_2h_3)$,则其在倒格子空间中的倒格矢的晶向指数为$[h_1h_2h_3]$
倒易点阵中由最短倒格矢$\vec{K}_{h_1h_2h_3}$表示的倒格点对应着正点阵中由晶面指数$(h_1h_2h_3)$所表征的晶面,以至于可以用一个倒格点来表示正点阵中的晶面,这种点(倒格点)与面(正点阵中的晶面)互为傅里叶的变换。
最短倒格矢的长度反比于晶面指数为$(h_1h_2h_3)$的晶面族的面间距$d_{h_1h_2h_3}$
\[\left|\vec{K}_{h_1h_2h_3}\right|=\frac{2\pi}{d_{h_1h_2h_3}}\]布里渊区
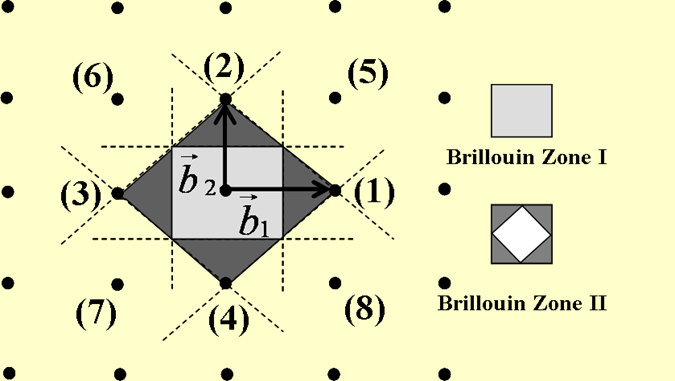
布里渊区划分法,基于倒易点阵的平移对称性而将整个倒格子空间分成第一、第二等一系列布里渊区,每个布里渊区的体积相同且和一个倒格点所占体积相等,因此,也是反映倒易点阵周期性的最小结构单元。
第一布里渊区的选取和倒格子空间的W-S原胞的选取完全相同,而第二、第三等布里渊区通过适当的平移对称操作,可以得到和第一布里渊区完全相同的凸多面体的形状。因此,布里渊区不仅作为最小结构单元能反映倒易点阵的周期性,而且还能充分反映倒易点阵的宏观对称性和平移对称性。
由于倒易点阵的平移对称性,因此,在固体物理学中对物理问题在倒格子空间的分析常常限于在第一布里渊区里进行,而对其它布里渊区的问题只需要通过平移对称操作就可得到。