以下是固体物理第二章相关内容
晶体的宏观特征
- 晶面规则的堆成配置
- 晶面角守恒
- 存在若干个晶面组合形成的晶带
- 晶体具有解理性
- 晶体具有确定的熔点
- 晶体具有物理性质的各向异性
- 晶体同时具有平移对称性和旋转对称性
晶体的微观特征
区别于其他固体,晶体最本质的特征是,构成晶体的粒子是按一定规则在空间三个方向上周期有序排列分布的,即具有微观结构的周期性。
典型的晶体结构
单原子晶体:
- 简单立方(SC),配位数6
- 体心立方(BCC),配位数8
- 面心立方(FCC),配位数12
- 六角密堆积(HCP),配位数12
- 金刚石结构
化合物晶体:
- NaCl型
- CsCl型
- CaF$_2$型
- ZnS型
- CaTiO$_3$型
空间点阵
晶体微观结构的研究包括两方面的内容:
- 晶体由何种原子通过何种结合方式凝聚到一起形成的?
- 这些原子在空间的排列方式如何?
我们主要讨论第二个问题,组成晶体的原子在空间是周期性地规则排列的,或称为长程有序。为描述晶体内部结构的长程有序,十九世纪人们引入“空间点阵”概念,在此基础上发展了布喇菲空间点阵学说。
空间点阵学说正确地反映了晶体内在结构长程有序的特征,其正确性为后来的晶体衍射所证明。在此之后,空间群理论又充实了空间点阵学说。
空间点阵学说的基本概念
基元
晶体可以由一种或多种原子(或离子)组成,它们构成晶体的基本结构单元,称为基元。将基元在空间中按一定方式作周期性平移对称操作就形成了具有一定结构的晶体。
格点
用位于原子平衡位置的几何点代表一个原子,结果得到一个与晶体几何特征相同、但无任何物理实质的几何图形。
结点
若选择晶体中任意一点,则晶体中一定存在无限多个和晶体相同周期性的点,空间点阵学说中所称的结点,代表着结构中相同的位置,是一种数学上的抽象。格点是特殊的结点。
点阵
结点在空间周期性排布的总体,称为空间点阵
晶格
如果用假想的线将点阵中的结点连接起来,则形成周期性排布的空间格架,点阵变成了网格。如果网格中的结点代表的是原子平衡位置所在的点,即格点,则形成的网格反映的是晶体中的原子周期性排布的特征。
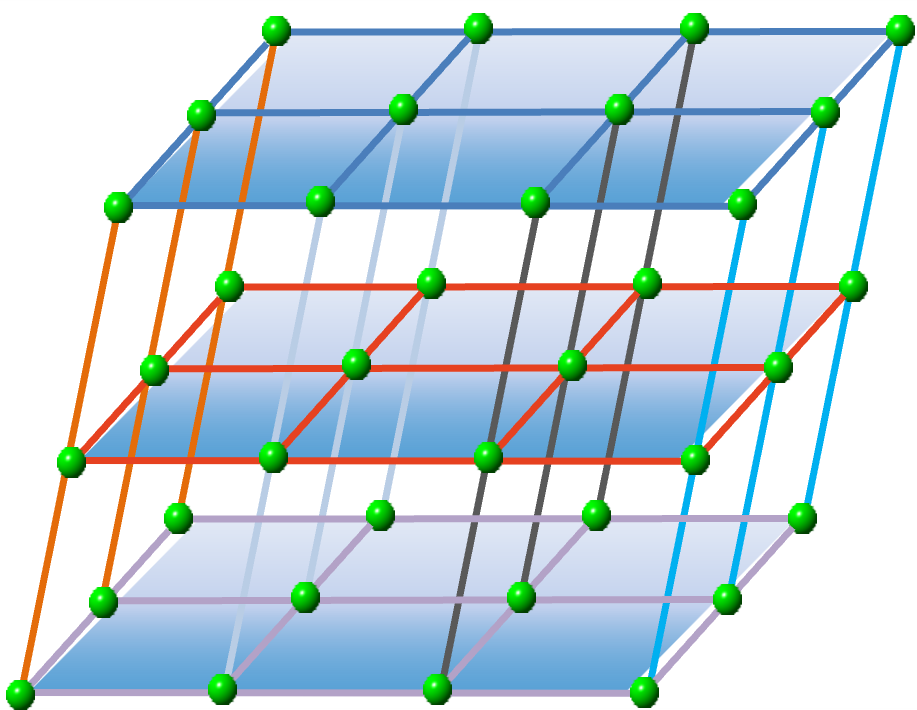
布喇菲格子和复式格子
如果晶体是由完全相同的一种原子周期性排布形成的单原子晶体,格点为原子平衡位置所在的几何点,这些格点在空间作周期性排布形成的格子称为布喇菲格子,也称简单格子。
如果晶体包含两种或两种以上的原子,则不同的原子各自构成自身的布喇菲格子(子晶格),若干个子晶格相互位移套构而形成所谓的复式格子。
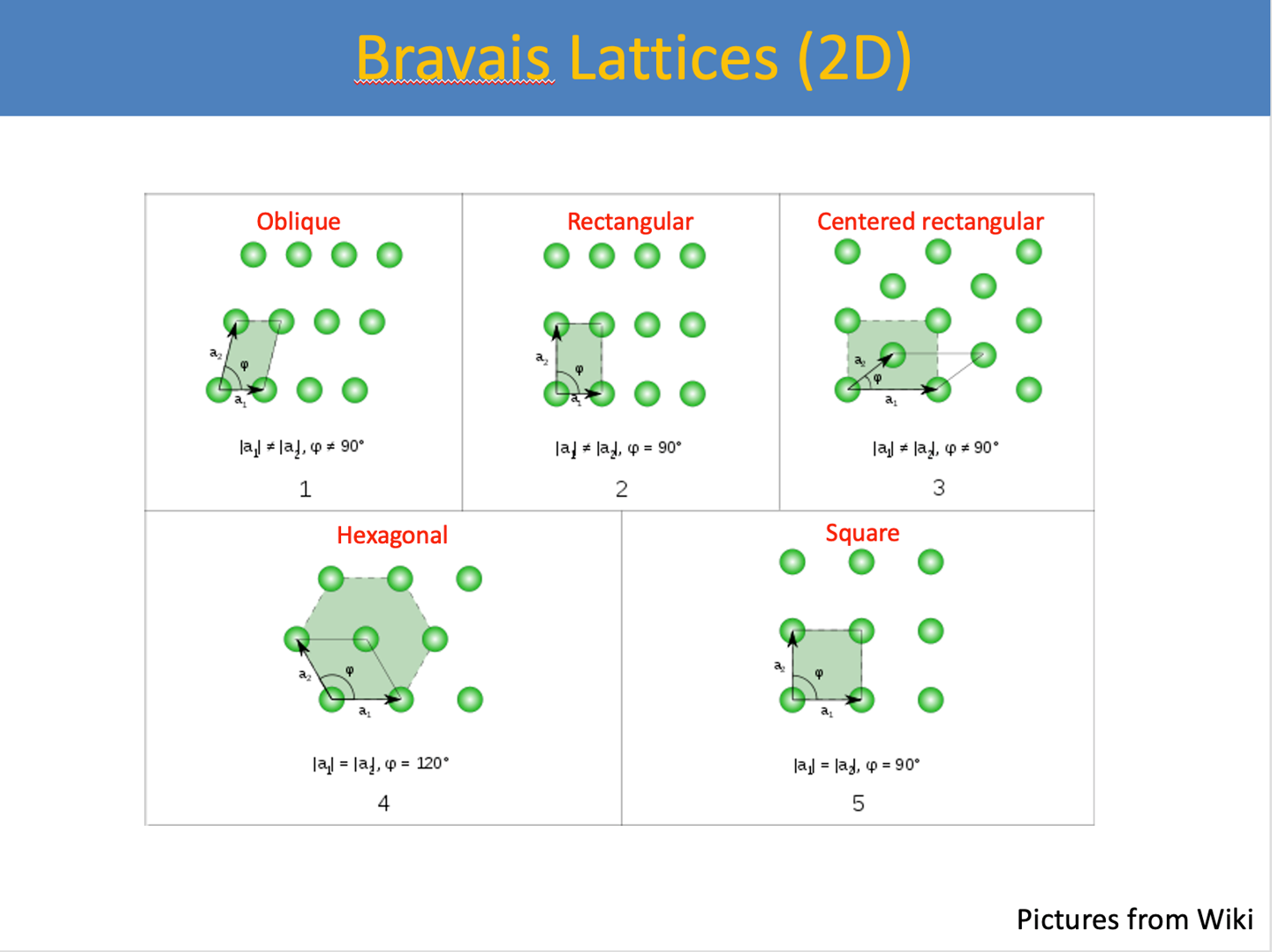
晶格的平移对称性
考虑空间任意一方向,由于晶格的周期性,该方向上的格点必呈周期性排列,周期为该方向上相邻格点间的间隔。这种周期性可以通过格点的平移对称操作来进行描述,即从所考虑的方向上任意一个格点开始,通过周期性平移,则在该方向上必能找到和该格点几何位置等价、周围环境相同的格点,这里所讲的周期性平移或者周期性重复排布的操作称为平移对称操作,相应的对称性称为平移对称性
晶体具有晶格周期性$\Leftrightarrow$晶体具有平移对称性
原胞和基矢
固体物理学原胞 (原胞):反应晶格周期性的最小重复单元。原子占据原胞顶角位置。对于单原子晶体,一 维长度最短、二维面积最小、三维体积最小的含有一个原子的重复单元。
基矢:原胞的边矢量$\vec{a_1},\vec{a_2},\vec{a_3}$,三个基矢的长度为三个基矢方向上的周期。
原胞的体积即一个原子所占体积:$\Omega=\vec{a}_1\cdot\vec{a}_2\times\vec{a}_3$
晶胞和基矢
结晶学原胞 (晶胞):既反应晶格周期性又反应晶体自身特殊对称性的最小重复单元。
基矢:晶胞的边矢量用$\vec{a},\vec{b},\vec{c}$表示
W-S原胞
W-S原胞:以一个格点为原点,作原点与其它格点连接的中垂面(或中垂线),由这些中垂面(或中垂线)所围成的最小体积(或面积)即是W-S原胞
特点:
- 只有原胞中心有格点,原胞顶点没有格点
- 一个原胞只有一个格点,因此,是最小的重复单元
- 将原胞沿中心格点到各个格点连线方向作周期性平移对称操作,同样可以不重叠地填满整个晶格而不留任何空隙,因此, W-S原胞可以反映晶格周期性
晶列和晶面
晶列
晶列:通过任何两个格点连一直线,则这直线上包含无限个周期分布的格点,周期为该直线上两相邻格点的间距这样的直线称为晶体的晶列。
晶列族:每一个晶列之外有无限个和该晶列平行且具有相同周期的晶列,在一个平面中相邻晶列间距离相等,这些相互平行且等间距分布的晶列称为晶列族
晶向:晶列的取向简称为晶向。
晶向指数:用来表征晶列取向的指数,任何一个格点A的位置矢量可以用$\vec{R}_l=l_1\vec{a}_1+l_2\vec{a}_2+l_3\vec{a}_3$表示,我们用$[l_1,l_2,l_3]$来表示晶列方向,称之为晶向指数,此时三者必须互质
晶列指数:在结晶学中,格点可以表示成$\vec{R}=m^{\prime}\vec{a}+n^{\prime}\vec{b}+p^{\prime}\vec{c}$,则$[m n p]$称为晶列指数,三者必须为互质整数。晶向指数表现的是原胞,晶列指数表现的是晶胞
晶面
晶面:通过晶格中任意三个非共线格点作一平面,会形成一个包含无限多个周期性排布的格点的二维平面网格,通常称为晶面
晶面族:与晶列族类似,在一晶面外过其它格点作一系列与原晶面平行的晶面,可得到无限多个等间距相互平行的晶面,各晶面上格点的分布情况是完全相同的,这些等间距相互平行的晶面称为一族晶面。所有的格点都在一族平行的晶面上而无遗漏。
晶面指数:如下图所示,最靠近原点的晶面在三个基矢上的截距为:$\frac{a_1}{h_1},\frac{a_2}{h_2},\frac{a_3}{h_3}$,则称$(h_1 h_2 h_3)$为晶面指数,其中三者互质
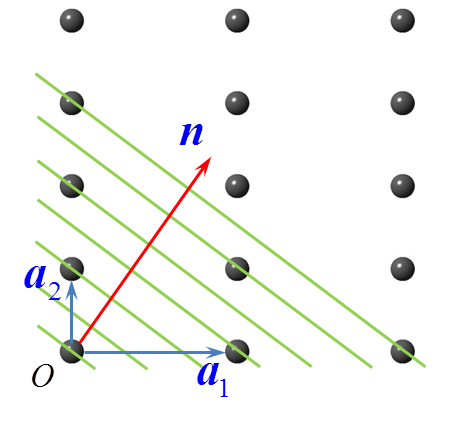
密勒指数:对于晶胞对应的晶面指数称为密勒指数
晶体的宏观对称性及其对称操作
8种基本的宏观对称操作:$1,2,3,4,6,i,m,\bar{4}$
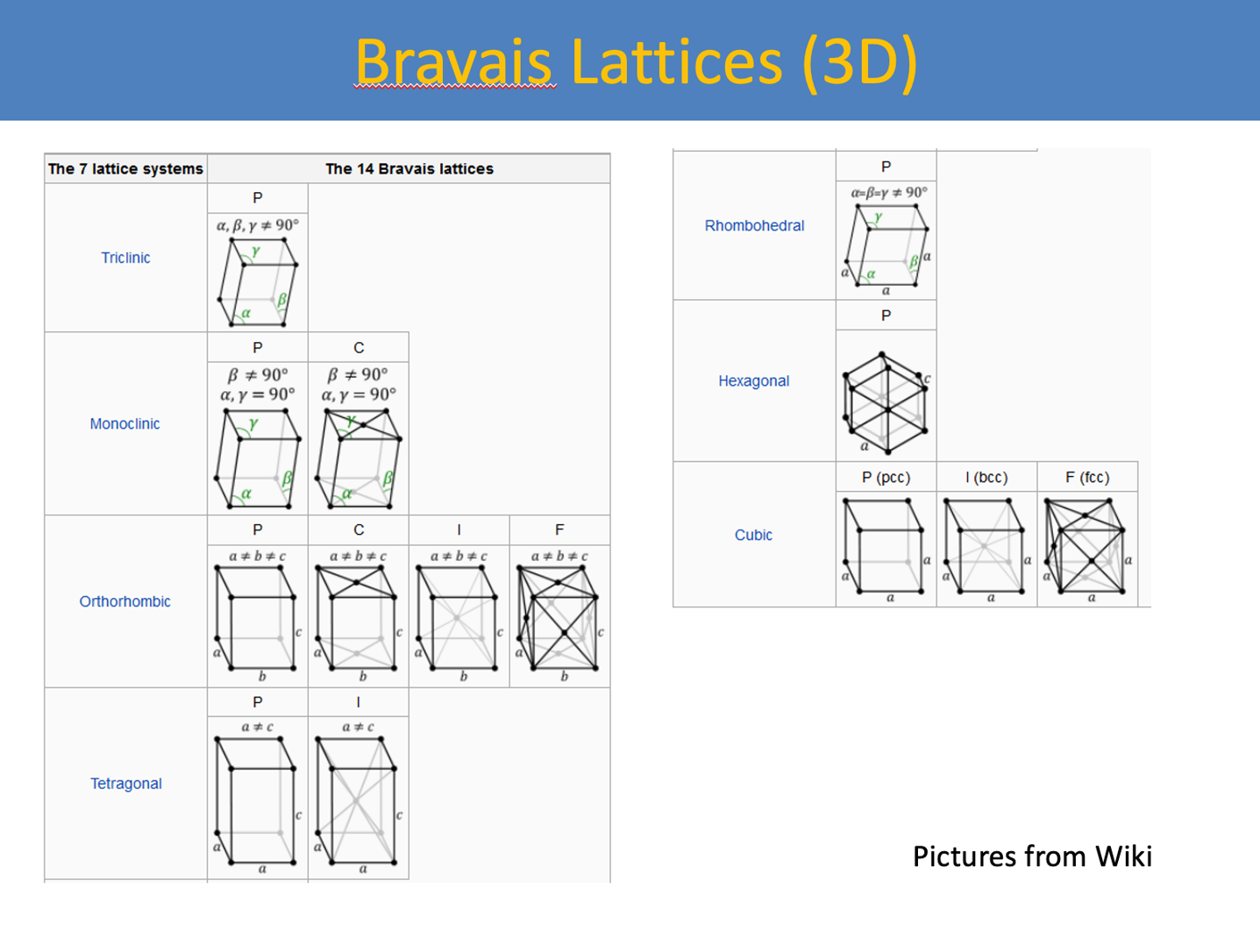
七大晶系
- 三斜:$a\neq b\neq c, \alpha\neq\beta\neq\gamma $
- 单斜:$a\neq b\neq c, \alpha=\beta=90^\circ\neq\gamma $
- 正交: $a\neq b\neq c, \alpha=\beta=\gamma=90^\circ $
- 四方: $a=b\neq c, \alpha=\beta=\gamma=90^\circ $
- 立方: $a=b=c, \alpha=\beta=\gamma=90^\circ $
- 六角: $a=b\neq c, \alpha=\beta=90^\circ, \gamma=120^\circ $
- 三角: $a=b=c, \alpha=\beta=\gamma\bot\neq90^\circ $