以下是固体物理第五章的内容
原子振动
在前面四章中,我们将原子看作在其平衡位置上不动,以使得整个晶体的势能最低,但是实际上不是的,原子在平衡位置附近做振动
一维单原子晶体的晶格振动
一维单原子晶体的振动解
由$N$个质量为$m$的原子,周期性排列形成一维原子链,周期为$a$,用$x_n$表示第$n$个原子离开平衡位置的位移,则第$n+1$个原子和第$n$个原子的相对位移为$\delta=x_{n+1}-x_n$,则相互作用能变为$U(r)=U(a+\delta)$
恢复力为$f(\delta)=-\beta\delta $,其中$\beta=\left(\frac{\mathrm{d}^2U}{\mathrm{d}\delta^2}\right)_{\delta=0}$
\[f_n=f(x_{n+1})+f(x_{n-1})=\beta(x_{n+1}-x_n)-\beta(x_n-x_{n-1})=\beta(x_{n+1}+x_{n-1}-2x_n)\]则运动方程为:
\[m\ddot{x}_n=\beta(x_{n+1}+x_{n-1}-2x_n)\]尝试解为:
\[x_n=Ae^{i(qna-\omega t)}\]带入可得色散关系:
\[\omega=2\sqrt{\frac\beta m}\left|\sin\frac{qa}2\right|\]格波
色散关系中不包含$n$,所有的原子都以相同的频率$\omega$振动。或者说,所有原子在作集体振动,表现为晶格振动。
晶格振动以平面波的形式在晶体中传播,这种描述晶格振动的波称为晶格振动波,简称格波。
由于一维单原子链仅有一种色散关系,这个格波称为声学波
相速度:
\[v_p=\frac{\omega}{q}=\frac{2}{q}\sqrt{\frac{\beta}{m}}\left|\sin\frac{qa}{2}\right|\]群速度:$v_g=\frac{\mathrm{d}\omega}{\mathrm{d}q}=a\sqrt{\frac\beta m}\cos\frac{qa}2$
长波极限(布里渊区中心):$q\rightarrow0$
\[\omega=2\sqrt{\frac\beta m}\frac{qa}2=qa\sqrt{\frac\beta m}\]短波极限(布里渊区边界):$q\to\pm\pi/a$
\[v_{p}=\frac{2a}{\pi}\sqrt{\frac{\beta}{m}}\neq0\\v_{g}=0\]为驻波
波恩-卡门边界条件
对于一个有限长原子链,链端的原子和内部原子明显不同,当只考虑近邻作用时,内部原子受到左右两个近邻原子的作用,而链端原子只受到一个近邻原子的作用,因此,内部原子和链端原子的运动方程会不同。
波恩-卡门假设:在一个长度为$L=Na$的有限晶体外仍然有无限多个相同的晶体,且各块晶体内相对应的原子的运动情况相同。
设想的晶体和有限尺寸的实际晶体,虽然两者原子势有差别,但由于原子间相互作用是短程的,差别可忽略不考虑。
玻恩-卡门周期性边界条件也可理解为,将一个长度为$L=Na$的原子链首尾相接成闭合环。
\[\begin{cases}x_1=Ae^{i(qa-\omega t)}\\x_{N+1}=Ae^{i[q(N+1)a-\omega t]}\end{cases}\quad\Rightarrow\quad e^{iqNa}=1\quad\Rightarrow\quad qNa=2\pi l\quad(l=0,\pm1,\pm2,\cdots)\]表征原子振动的波矢 $q$ 具有分立的取值 (量子化)
\[q=\frac{2\pi l}{Na}\quad(l=0,\pm1,\pm2,\cdots)\]我们主要考虑第一布里渊区内的值$-\frac\pi a<q\leq\frac\pi a\to - \frac{N}{2}<l\leq\frac{N}{2}$
易得$l$共有$N$个取值,即一个布里渊区里波矢数目等于原胞数$N$,一个振动波矢对应一个振动频率,每一个频率代表一个格波,格波数等于晶体的总自由度
一维多原子的晶格振动
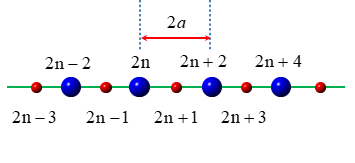
考虑由$N$个原胞周期性排列形成的一维原子链,周期为$2a$,每个原胞含有一个大原子(质量$M$)和一个小原子(质量$m$)
仅考虑最近邻的作用,有
\[f(x_{2n+1})=\beta(x_{2n+2}-x_{2n+1})-\beta(x_{2n+1}-x_{2n})=\beta(x_{2n+2}+x_{2n}-2x_{2n+1})\] \[f(x_{2n+2})=\beta(x_{2n+3}-x_{2n+2})-\beta(x_{2n+2}-x_{2n+1})=\beta(x_{2n+3}+x_{2n+1}-2x_{2n+2})\]则写出其动力学方程
\[m\ddot{x}_{2n+1}=\beta(x_{2n+2}+x_{2n}-2x_{2n+1})\] \[M\ddot{x}_{2n+2}=\beta(x_{2n+3}+x_{2n+1}-2x_{2n+2})\]写出其尝试解:
\[x_{2n+1}=Ae^{i[q(2n+1)a-\omega t]}\] \[x_{2n+2}=Be^{i[q(2n+2)a-\omega t]}\]带入原方程可得
\[(2\beta-m\omega^2)A-(2\beta\cos qa)B=0\\(-2\beta\cos qa)A+(2\beta-M\omega^2)B=0\]这个方程非0解的要求是系数行列式非零,则
\[\begin{vmatrix}2\beta-m\omega^2&2\beta\cos qa\\-2\beta\cos qa&2\beta-M\omega^2\end{vmatrix}=0\]得到色散关系:
\[\omega^2=\frac\beta{mM}\left\{\left(m+M\right)\pm\left[m^2+M^2+2mM\cos2qa\right]^{\frac12}\right\}\]一种色散关系对应一支独立的格波,一维双原子链中有两支独立格波的存在。一支称为光学波(取+),一支称为声学波(取-)
光学波反应了原胞内不同原子之间的相对振动
\[\omega_{+}^{2}=\frac{\beta}{mM}\left[(m+M)+\sqrt{m^{2}+M^{2}+2mM\cos(2qa)}\right]\\\sqrt{\frac{2\beta}{m}}\leq\omega_{+}\leq\sqrt{\frac{2\beta}{\mu}}\\\mu=\frac{mM}{m+M}\]声学波反应了原胞质心的振动,即原胞整体的振动。
\[\omega_{-}^{2}=\frac{\beta}{mM}\left[(m+M)-\sqrt{m^{2}+M^{2}+2mM\cos(2qa)}\right]\\0\leq\omega_{-}\leq\sqrt{\frac{2\beta}M}\]能看到$\omega_{+,min}>\omega_{-,max}$,这代表光学波的格波频率综述比声学波高,两支波之间出现了频率的禁带,在布里渊区边界,频率禁带宽度为:
\[\Delta\omega=\omega_{+,\min}-\omega_{-,\max}=\sqrt{2\beta}\Bigg(\sqrt{\frac1m}-\sqrt{\frac1M}\Bigg)\]波恩-卡门边界条件
将玻恩-卡门周期性边界条件应用于双原子链,则可以认为在一个由$N$个原胞构成的有限长的原子链外,仍然有无限多个相同的原子链,如果将小原子放在$1,3,5\cdots(2N-1)$奇数格点上,按玻恩-卡门周期性边界条件,则第一个原胞中位于格点$1$的小原子和第$N+1$个原胞中位于格点$2N+1$ 的小原子属于同一个原子
与一维单原子类似,首尾连接成环,有
\[\begin{cases}x_1=Ae^{i(qa-\omega t)}\\x_{2N+1}=Ae^{i[q(2N+1)a-\omega t]}\end{cases}\quad\Rightarrow\quad e^{i2qNa}=1\quad\Rightarrow\quad qNa=\pi l\quad(l=0,\pm1,\pm2,\cdots)\] \[q=\frac{\pi l}{Na}\quad(l=0,\pm1,\pm2,\cdots)\] \[-\frac{\pi}{2a}<q\leq\frac{\pi}{2a}\\\quad\\-\frac{N}{2}<l\leq\frac{N}{2}\]$l$取$N$个分立的值
三维多原子晶体的振动
我们可以将一维的振动推广到三维情况
假设一个三维晶体由$N$个原胞组成,按照一维的结论:
晶格振动波矢数=晶体原胞数,晶格振动频率数=晶体自由度数
则三维晶体一个布里渊区总共有$N$个振动波矢的数目,三维晶体一个布里渊区总共有$3nN$个晶格振动的频率,三维晶体格波总数为$3nN$ ,声学波有3支,反映原胞整体的振动,1个纵波和2个横波,剩下的$3(n-1)$支是光学波,反映原胞内原子之间的相对振动。
简谐振动的量子理论
简谐振动的量子理论构造的基本思路:
- 构造和简谐振动相对应的哈密顿算符
- 通过表象变换,即从坐标表象变换到状态表象,以消除哈米顿算符中包含两两原子坐标的交叉项
- 讨论格波的能量及其量子化,进而引入声子的概念
为简单起见,仅以一维单原子晶格振动为例加以分析和讨论,所采用的方法和得到的结论可直接推广到三维情况。
哈密顿算符
对于一维单原子晶体,有:
\[U=\frac12\beta\sum_n(x_{n-1}-x_n)^2\\T=\frac12\sum_nm(\frac{dx_n}{dt})^2=\frac12\sum_nm\dot{x}_n^2\\ \hat{H}=\hat{T}+\hat{U}\]从数学角度,由于晶格振动是晶体中大量原子的集体振动,总哈密顿量应是所有原子的坐标和速度的函数,因此,哈密顿量中必包含两两原子坐标的交叉项
\[\begin{aligned} U&=\frac12\beta\sum_n\left(x_{n-1}-x_n\right)^2=\frac12\beta\sum_n\left(x_{n-1}-x_n\right)^*\left(x_{n-1}-x_n\right) \\ &=\frac12\beta\sum_n\left(x_{n-1}^2+x_n^2-x_n^*x_{n-1}-x_{n-1}^*x_n\right) \end{aligned}\]交叉项的出现正是原子振动相互耦合的反映 ,上面的哈密顿算符是以原子位移坐标为基础而建立的,以此为基础的描述是坐标表象中的描述 ,通过表象变换,即从坐标表象变换成新的表象(状态表象),若能消除哈密顿算符中两两原子坐标的交叉项,则可以将晶格振动的总能量表述为独立简单振子能量之和
表象变换
我们以$\left[\frac1{\sqrt{N}}e^{inaq}\right]$作为基矢,构造一个新的坐标系,则有:
\[x_{n}(t)=\sum_{q}w_{q}(t)\frac{1}{\sqrt{N}}e^{inaq} \\ w_{q}(t)=\sum_{n}x_{n}(t)\frac{1}{\sqrt{N}}e^{-inaq}\]我们使用$w$来表示动能和势能,则有
\[\begin{aligned} U&=\frac{1}{2} \beta\sum_{n}(x_{n-1}^{2}+x_{n}^{2}-x_{n-1}^{*}x_{n}-x_{n}^{*}x_{n-1}) \\ &=\frac{1}{2} \beta\sum_{q}w_{q}^{2}(2-e^{iaq}-e^{-iaq}) \\ &=\frac12\beta\sum_qw_q^22(1-\cos qa) \\ &=\sum_q\frac12m\omega_q^2w_q^2\\ T&=\frac12\sum_qm(\frac{dw_q}{dt})^2=\sum_q\frac{P_q^2}{2m} \end{aligned}\]则哈密顿算符为:
\[\hat{H}_q=\frac{\hat{P}_q^2}{2m}+\frac12m\omega_q^2\hat{w}_q^2\]$\hat{w_q}$称为状态表象中的原子位移坐标算符,新的原子位移坐标算符已不再只和个别原子相联系,而是代表$N$个原子的集体运动,是一种集体原子位移坐标算符
则本征能量为:
\[\varepsilon_q=\left(n_q+\frac{1}{2}\right)\hbar\omega_q\]总能量为:
\[\varepsilon=\sum_q\varepsilon_q=\sum_q\left(n_q+\frac{1}{2}\right)\hbar\omega_q\]声子
由上可知,对于格波,其能量是量子化的,最小的能量单元为$\hbar\omega_q$, 声子服从玻色-爱因斯坦分布:
\[\langle n_q\rangle=\frac1{e^{\beta\hbar\omega_q}-1}\]晶格振动能为:
\[E=\sum_q\langle n_q\rangle\hbar\omega_q=\sum_q\frac{\hbar\omega_q}{e^{\beta\hbar\omega_q}-1}\]声子可以被产生和湮灭,当电子、光子等粒子与声子发生相互作用时,将会交换以$\hbar\omega_q$为单位的能量,使格波跃迁。
在实际的研究中,特别是理论研究中,人们习惯通过声子频率的分布函数(亦称为晶格振动模式密度函数)的引入对晶格振动及其相关问题进行研究,声子频率的分布函数习惯上称之为声子谱
晶格振动的比热理论
经典模型(19世纪初)
根据能量均分定理,$\bar{E}=3nNk_BT$,则有杜隆-珀替定律
\[C_V=\left(\frac{\partial\bar{E}}{\partial T}\right)_V=3nNk_B\]即比热是温度无关的常数,但是实验表明,低温下比热随温度降低而快速趋向于0,和杜隆-珀替定律完全不同,说明问题并非象经典理论所考虑的那样简单。
爱因斯坦模型(1907 A.D.)
爱因斯坦提出,晶体中每个原子都以相同频率$\omega_E$振动,借用普朗克光量子的概念,提出原子振动的能量量子为$\hbar\omega_E$,考虑三维晶体,每一个原子沿三个方向的振动可以看成三个独立的振子,整个系统有$3nN$个振子,设第$j$个的振子的能量为$\varepsilon_j$则系统平均的热振动能为:
\[\bar{E}(T)=\sum_i^{3nN}\frac{\hbar\omega_i}{e^{\beta\hbar\omega_i}-1}=\frac{3nN\hbar\omega_E}{e^{\hbar\omega_E/k_BT}-1}\]晶格比热为:
\[C_V=\left(\frac{\partial\bar{E}}{\partial T}\right)_V=3nNk_B\left(\frac{\hbar\omega_E}{k_BT}\right)^2\frac{e^{\hbar\omega_E/k_BT}}{\left(e^{\hbar\omega_E/k_BT}-1\right)^2}\]其中定义爱因斯坦热容函数:
\[f_{B}\left(\frac{\hbar\omega_{E}}{k_{B}T}\right)=\left(\frac{\hbar\omega_{E}}{k_{B}T}\right)^{2}\frac{e^{\hbar\omega_{E}/k_{B}T}}{\left(e^{\hbar\omega_{E}/k_{E}T}-1\right)^{2}}\]定义爱因斯坦温度:
\[\theta_E=\frac{\hbar\omega_E}{k_B}\]则
\[f_B\left(\frac{\hbar\omega_E}{k_BT}\right)=f_B\left(\frac{\theta_E}T\right)=\left(\frac{\theta_E}T\right)^2\frac{e^{\theta_E/T}}{\left(e^{\theta_E/T}-1\right)^2}\\C_V=3nNk_Bf_B\left(\frac{\theta_E}T\right)\]在高温极限下,$C_V\approx 3nNk_B$
在低温极限下,$C_V\approx 3nNk_B\left(\frac{\theta_E}T\right)^2e^{-\theta_E/T}$
爱因斯坦模型预言的低温下晶格比热随温度降低按温度的指数形式趋于0,是经典理论所不能得到的结果,解决了长期以来困扰物理学的一个疑难问题,这正是爱因斯坦模型的重要贡献所在。
但是它忽略了各个振子振动频率的差别以及对比热贡献的差异,或者说,爱因斯坦模型中只考虑了一种频率的振子对晶格比热的贡献。
德拜模型(1912 A.D.)
如果对爱因斯坦模型稍加改进,即每个原子的振动仍可看成是三个方向独立振动的振子,但所有振子并不是以相同频率振动,而是第j个振子以频率$\omega_j$振动,相应的振子能量为$\varepsilon_j=\hbar\omega_j$
则有
\[E(T)=\sum_{j=1}^{3nN}\frac{\hbar\omega_j}{e^{\hbar\omega_j/k_\text{B}T}-1}\]德拜提出两个假设:
- 低温下晶格振动主要为$\omega<\omega_m$的低频振动,而高频振动基本可忽略,这里的$\omega_m$称为德拜频率
- 由于低的振动频率对应的是长声学波,因此,三维晶格可视为连续介质,相应的格波可看成是弹性波,由于这一原因,德拜近似又称为弹性波近似
则
\[E(T)=\sum_j^{3N}\frac{\hbar\omega_j}{e^{t\omega_j/k_2T}-1}=\int_0^\infty\frac{\hbar\omega}{e^{t\omega/k_2T}-1}g(\omega)d\omega\approx\int_0^{a_m}\frac{\hbar\omega}{e^{t\omega/k_3T}-1}g(\omega)d\omega\]其中$g(\omega)$称为声子谱函数。
对于每一个波矢,有三支声学波,一支纵波,两支横波
\[\omega=\nu_{l}q\quad\left|\nabla_{q}\omega(\vec{q})\right|=\nu_{l}\\\omega=\nu_{t}q\quad\left|\nabla_{q}\omega(\vec{q})\right|=\nu_{t}\]由此可得声子谱函数:
\[\begin{aligned} g(\omega)&=\frac{V}{\left(2\pi\right)^{3}}\int\frac{ds}{\left|\nabla_{\vec{q}}\omega(\vec{q})\right|}=\frac{V}{\left(2\pi\right)^{3}}(\frac{1}{\nu_{l}}\times\int_{S_{\omega}}ds+2\times\frac{1}{\nu_{t}}\times\int_{S_{\omega}}ds) \\ &=\frac{V}{\left(2\pi\right)^{3}}(\frac{1}{\nu_{l}}\times4\pi q^{2}+2\times\frac{1}{\nu_{t}}\times4\pi q^{2}) \\ &=\frac V{\left(2\pi\right)^3}\times(\frac1{\nu_1^3}\times4\pi\omega^2+2\times\frac1{\nu_t^3}\times4\pi\omega^2) \\ &=\frac{V}{\left(2\pi\right)^{3}}\times\frac{3}{\overline{\nu}^{3}}\times4\pi\omega^{2} \\ &=\frac{3V}{2\pi^{2}\overline{\nu}^{3}}\omega^{2} \end{aligned}\]则有
\[3N=\int_0^\infty g(\omega)d\omega\approx\int_0^{\omega_m}g(\omega)d\omega=\frac{3V}{2\pi^2\overline{\nu}^3}\int_0^{\omega_m}\omega^2d\omega\]可得到德拜频率$\omega_m$:
\[\omega_m=\overline{\nu}\left[6\pi^2\left(\frac NV\right)\right]^{1/3}=\overline{\nu}\left[6\pi^2n\right]^{1/3}\]则得到平均振动能和晶格比热:
\[\begin{aligned}&E(T)=\frac{3V}{2\pi^2\overline{\nu}^3}\int_0^{\omega_m}\frac{\hbar\omega^3}{e^{\hbar\omega/k_2T}-1}d\omega\\&C_V=\frac{3V}{2\pi^2\overline{\nu}^3}\int_0^{\omega_m}k_B\left(\frac{\hbar\omega}{k_BT}\right)^2\frac{e^{\hbar\omega/k_2T}}{\left(e^{\hbar\omega/k_2T}-1\right)^2}\omega^2d\omega\end{aligned}\]定义德拜温度$\theta_D=\frac{\hbar \omega_m}{k_B}$
令$\xi{=}\hbar\omega/k_{B}T$,则
\[C_V=9Nk_B\left(\frac T{\theta_D}\right)^3\int_0^{\theta_D/T}\frac{\xi^4e^\xi}{\left(e^\xi-1\right)^2}d\xi=3Nk_Bf_D(\frac T{\theta_D})\]其中$f_D$为德拜比热函数。
高温极限下符合经典理论,低温极限下,
\[C_V=\frac{12\pi^4Nk_B}5{\left(\frac T{\theta_D}\right)^3}\]符合实验结论
晶格比热的量子理论(1913 A.D.)
\[\begin{aligned} \bar{E}&=\sum_{q}\frac{\hbar\omega_{q}}{e^{\beta\hbar\omega_{q}}-1}\\ C_{V}&=\left(\frac{\partial\bar{E}}{\partial T}\right)_{V}\\ &=-\frac{1}{k_{B}T^{2}}\left(\frac{\partial\bar{E}}{\partial\beta}\right)_{V}\\ &=\sum_{q}\frac{1}{k_{B}T^{2}}\frac{\hbar^{2}\omega_{q}^{2}e^{\beta\hbar\omega_{q}}}{\left(e^{\beta\hbar\omega_{q}}-1\right)^{2}}\\ &=\sum_{q}k_{B}\left(\frac{\hbar\omega_{q}}{k_{B}T}\right)^{2}\frac{e^{\hbar\omega_{q}/k_{B}T}}{\left(e^{\hbar\omega_{q}/k_{B}T}-1\right)^{2}} \end{aligned}\]高温极限与经典理论相同
低温极限下,
\[C_V=k_B\sum_q\left(\frac{\hbar\omega_q}{k_BT}\right)^2e^{-\hbar\omega_q/k_BT}\]与实验定性是一致的。