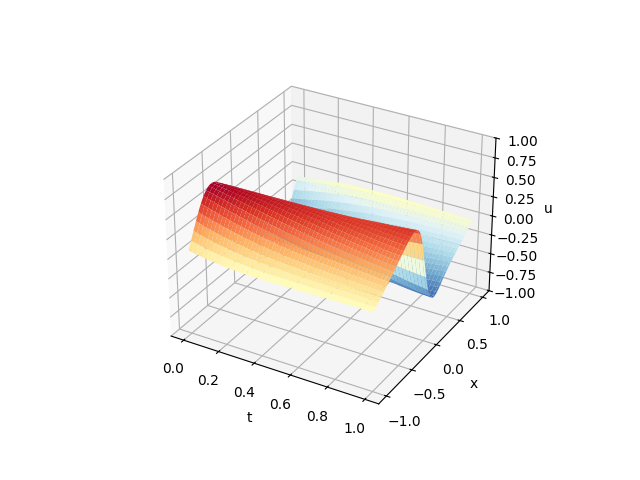
调研了PINN的简单使用
PDE的求解
PDE有多种求解方式，包括有限差分法、有限元法在内的网格法以及Kansa法、移动最小二乘法在内的无网格法。
网格法主要使用网格对偏微分方程进行离散化，在网格上使用数值微分求解。
无网格法主要是使用近似函数对原函数进行近似，然后使用PDE的条件对原函数进行拟合的方法。
在传统方法中，无论是网格法还是无网格法，均使用数值微分对PDE进行求解，但是数值微分本身存在误差，而且在无网格法中，由于我们会预设基函数来对原函数进行拟合，这也存在误差，因此在传统方法中，网格法相较于无网格法更容易实现的同时还具有更低的误差，因此目前常见的PDE求解器使用的方法均为网格法。
但是如果去除了数值微分的误差影响，在近似函数取得较为复杂的情况下，无网格法理论上较于网格法会具有更高的精确度，而PINN就是采用精确微分求解PDE的一种无网格法
自动微分
自动微分基于链式法则,将复杂函数分解为基本运算的组合,然后逐步计算每个基本运算的导数并累积。它通过跟踪计算图中的数值流动来实现导数计算。
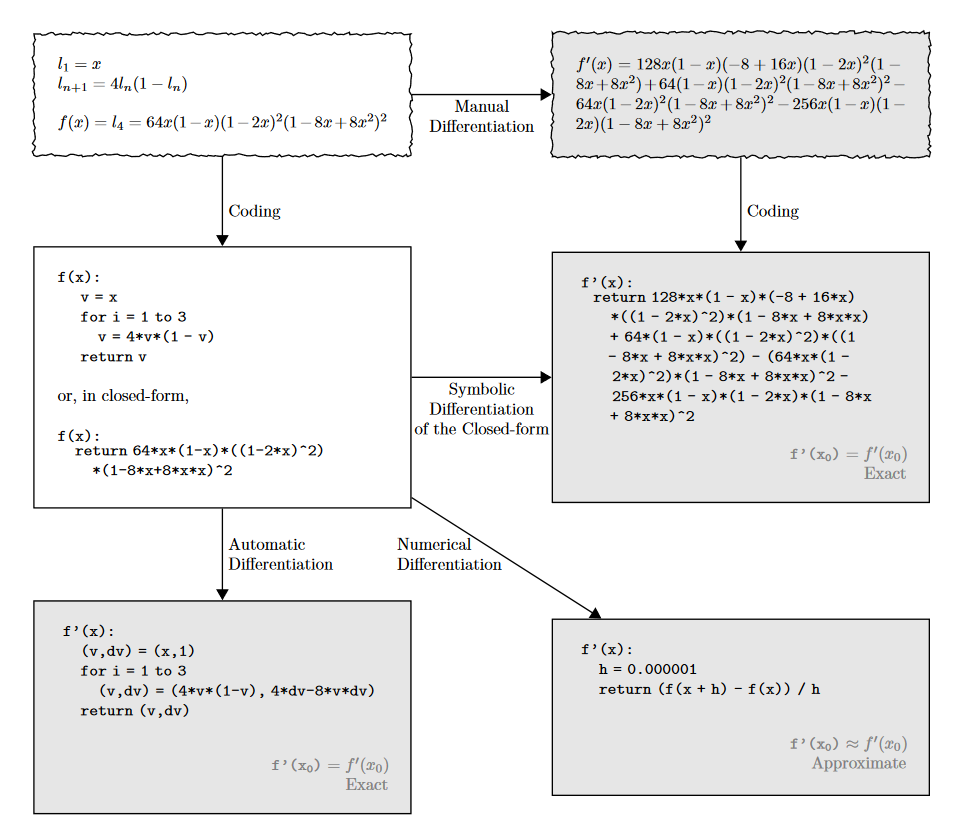图源：Automatic differentiation in machine learning: a survey
由此可见，自动微分显然是一种精确微分。自动微分需要一种函数，这种函数最好是由大量的$\omega x + b$复合而成，这样我们就可以通过链式法则对复合函数进行求导，从而得到精确的导数。
显然，自动微分天生契合神经网络的结构，因此自动微分广泛运用在神经网络的反向传播之中。
PINN
内嵌物理信息神经网络显然具有两部分，一部分是PI，也就是物理信息，另一部分则是NN，也就是神经网络。
考虑到无网格法的核心是找到近似函数，在PINN中，我们使用神经网络作为近似函数(因而考虑到网络的复杂性，这个近似函数往往只有网络的形式)，这就是NN，使用边界条件、初始条件作为损失函数，这就是PI，训练后的网络，即我们的PDE的解。
我们以一个简单的例子来说明PINN的原理。
\[\left.\left\{\begin{array}{l}u_t+u\times u_x-w\times u_{xx}=0\\u(0,x)=-sin(\pi x)\\u(t,\quad1)=0\\u(t,-1)=0\\w=\frac{0.01}\pi,x\in(-1,1),t\in(0,1)\end{array}\right.\right.\]在PINN中，我们往往使用MLP作为神经网络，我们使用torch构造一个网络结构
class MLP(nn.Module):
def __init__(self, NN):
super(MLP, self).__init__()
self.input_layer = nn.Linear(2, NN)
self.hidden_layer1 = nn.Linear(NN,int(NN/2))
self.hidden_layer2 = nn.Linear(int(NN/2), int(NN/2))
self.output_layer = nn.Linear(int(NN/2), 1)
def forward(self, x):
out = torch.tanh(self.input_layer(x))
out = torch.tanh(self.hidden_layer1(out))
out = torch.tanh(self.hidden_layer2(out))
out_final = self.output_layer(out)
return out_final
然后我们写一下方程，作为约束条件：
def pde(x, net):
u = net(x)
u_tx = torch.autograd.grad(u, x, grad_outputs=torch.ones_like(net(x)),
create_graph=True, allow_unused=True)[0]
d_t = u_tx[:, 0].unsqueeze(-1)
d_x = u_tx[:, 1].unsqueeze(-1)
u_xx = torch.autograd.grad(d_x, x, grad_outputs=torch.ones_like(d_x),
create_graph=True, allow_unused=True)[0][:,1].unsqueeze(-1)
w = torch.tensor(0.01 / np.pi)
return d_t + u * d_x - w * u_xx
定义一下我们的损失函数形式和优化器：
mse_cost_function = torch.nn.MSELoss(reduction='mean') # Mean squared error
optimizer = Lion(net.parameters(), lr=1e-4)
特别的，我们使用Lion作为优化器，其具有非常好的优化效果，能显著降低迭代步数。
然后写一下我们的训练函数：
t_bc_zeros = np.zeros((2000, 1))
x_in_pos_one = np.ones((2000, 1))
x_in_neg_one = -np.ones((2000, 1))
u_in_zeros = np.zeros((2000, 1))
iterations = 3000
for epoch in range(iterations):
optimizer.zero_grad()
t_in_var = np.random.uniform(low=0, high=1.0, size=(2000, 1))
x_bc_var = np.random.uniform(low=-1.0, high=1.0, size=(2000, 1))
u_bc_sin = -np.sin(np.pi * x_bc_var)
pt_x_bc_var = Variable(torch.from_numpy(x_bc_var).float(), requires_grad=False)
pt_t_bc_zeros = Variable(torch.from_numpy(t_bc_zeros).float(), requires_grad=False)
pt_u_bc_sin = Variable(torch.from_numpy(u_bc_sin).float(), requires_grad=False)
pt_x_in_pos_one = Variable(torch.from_numpy(x_in_pos_one).float(), requires_grad=False)
pt_x_in_neg_one = Variable(torch.from_numpy(x_in_neg_one).float(), requires_grad=False)
pt_t_in_var = Variable(torch.from_numpy(t_in_var).float(), requires_grad=False)
pt_u_in_zeros = Variable(torch.from_numpy(u_in_zeros).float(), requires_grad=False)
# 求边界条件的损失
net_bc_out = net(torch.cat([pt_t_bc_zeros, pt_x_bc_var], 1)) # u(x,t)的输出
mse_u_2 = mse_cost_function(net_bc_out, pt_u_bc_sin) # e = u(x,t)-(-sin(pi*x))
net_bc_inr = net(torch.cat([pt_t_in_var, pt_x_in_pos_one], 1)) # 0=u(t,1)
net_bc_inl = net(torch.cat([pt_t_in_var, pt_x_in_neg_one], 1)) # 0=u(t,-1)
mse_u_3 = mse_cost_function(net_bc_inr, pt_u_in_zeros) # e = 0-u(t,1)
mse_u_4 = mse_cost_function(net_bc_inl, pt_u_in_zeros) # e = 0-u(t,-1)
x_collocation = np.random.uniform(low=-1.0, high=1.0, size=(2000, 1))
t_collocation = np.random.uniform(low=0.0, high=1.0, size=(2000, 1))
all_zeros = np.zeros((2000, 1))
pt_x_collocation = Variable(torch.from_numpy(x_collocation).float(), requires_grad=True)
pt_t_collocation = Variable(torch.from_numpy(t_collocation).float(), requires_grad=True)
pt_all_zeros = Variable(torch.from_numpy(all_zeros).float(), requires_grad=False)
f_out = pde(torch.cat([pt_t_collocation, pt_x_collocation], 1), net) # f(x,t)的输出
mse_f_1 = mse_cost_function(f_out, pt_all_zeros)
loss = mse_f_1 + mse_u_2 + mse_u_3 + mse_u_4
loss.backward()
optimizer.step()
with torch.autograd.no_grad():
if epoch % 100 == 0:
print(epoch, "Traning Loss:", loss.data)
求解过程如下：
0 Traning Loss: tensor(0.5126)
100 Traning Loss: tensor(0.4608)
200 Traning Loss: tensor(0.4518)
300 Traning Loss: tensor(0.4403)
400 Traning Loss: tensor(0.4373)
500 Traning Loss: tensor(0.4268)
600 Traning Loss: tensor(0.4031)
700 Traning Loss: tensor(0.3871)
800 Traning Loss: tensor(0.3683)
900 Traning Loss: tensor(0.3462)
1000 Traning Loss: tensor(0.3033)
1100 Traning Loss: tensor(0.2588)
1200 Traning Loss: tensor(0.2162)
1300 Traning Loss: tensor(0.1814)
1400 Traning Loss: tensor(0.1661)
1500 Traning Loss: tensor(0.1583)
1600 Traning Loss: tensor(0.1538)
1700 Traning Loss: tensor(0.1535)
1800 Traning Loss: tensor(0.1468)
1900 Traning Loss: tensor(0.1399)
2000 Traning Loss: tensor(0.1330)
2100 Traning Loss: tensor(0.1306)
2200 Traning Loss: tensor(0.1255)
2300 Traning Loss: tensor(0.1195)
2400 Traning Loss: tensor(0.1111)
2500 Traning Loss: tensor(0.1106)
2600 Traning Loss: tensor(0.1091)
2700 Traning Loss: tensor(0.1085)
2800 Traning Loss: tensor(0.1059)
2900 Traning Loss: tensor(0.1042)
最后我们画一下结果：
