调研了RAJA库的简单使用
RAJA安装
在使用RAJA的过程中出现了以下问题:
- 在启用CUDA的情况下,RAJA无法查找到所使用的CUDA版本,而在CUDA的安装位置也找不到
cuda-config.cmake,导致目前RAJA无法正常调用CUDA - 在启用OpenMP Target Offload的情况下,RAJA无法正常调用ptx,导致无法在Nvidia GPU上运行。
简单来说,目前安装的RAJA版本无法运行在GPU上,目前这些问题仍旧在解决中
原程序的OOP改造
在本来的程序中,我采用静态束定的方式对程序进行约束,虽然在宏观上静态束定可以很好的解决问题,但是考虑到实际程序的编写过程,使用静态束定不但无法利用OO的特性来简化程序的开发过程,无法提高代码的复用性,而且还会提高程序的复杂性,使后续的开发难度提升。
因此在当前还未使用RAJA对程序进行大范围的改写的时候,先抽象代码结构使其具有OO的特性,为后面的开发过程进行铺垫。
UML组织
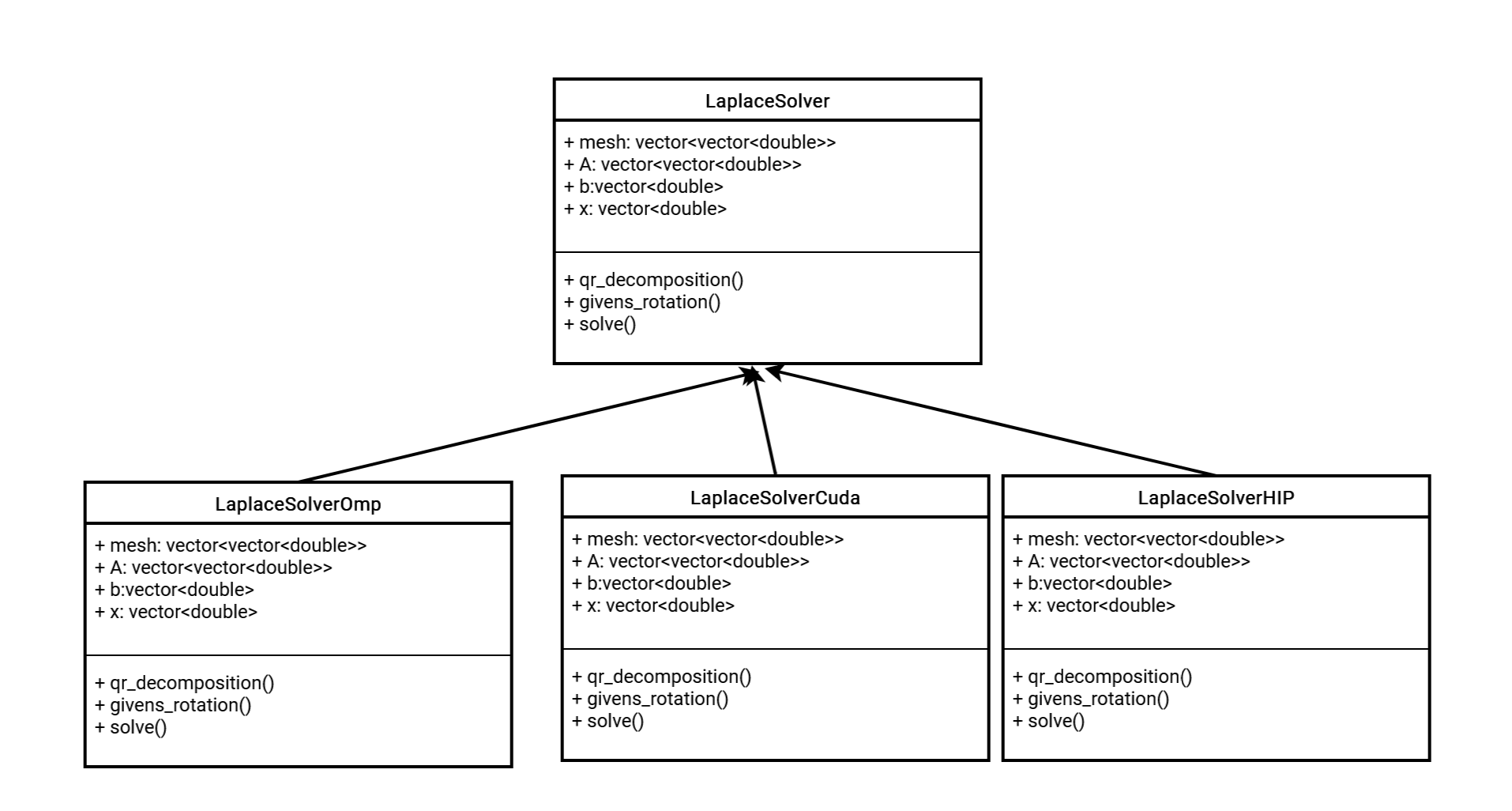
代码实际编写
基类
class LaplaceSolver{
protected:
virtual void givens_rotation(double a, double b, double &c, double &s)=0;
virtual void qr_decomposition(vector<vector<double>> &A, vector<vector<double>> &Q, vector<vector<double>> &R) =0;
vector<vector<double>> mesh;
vector<vector<double>> A;
vector<double> b;
vector<double> x;
public:
virtual std::vector<double> solve()=0;
vector getResult(){
return this->x
}
};
由于CUDA等待RAJA配置完成后再写,而OMP已经可以使用,所以下面的代码以OMP作为展示
实现类1:LaplaceSoverOMP
class LaplaceSolverOmp:LaplaceSolver{
private:
void givens_rotation(double a, double b, double &c, double &s) {
if (b == 0) {
c = 1;
s = 0;
} else {
if (abs(b) > abs(a)) {
double tau = -a / b;
s = 1 / sqrt(1 + tau * tau);
c = s * tau;
} else {
double tau = -b / a;
c = 1 / sqrt(1 + tau * tau);
s = c * tau;
}
}
}
void qr_decomposition(vector<vector<double>> &Q,vector<vector<double>> &R) {
int m = A.size();
int n = A[0].size();
Q.assign(m, vector<double>(m, 0));
R = A;
RAJA::forall<RAJA::omp_parallel_for_exec>(RAJA::TypedRangeSegment<int>(0,m),[=](int i){
Q[i][i] = 1;
});
for (int j = 0; j < n; j++) {
for (int i = j + 1; i < m; i++) {
double c, s;
givens_rotation(R[j][j], R[i][j], c, s);
RAJA::forall<RAJA::omp_parallel_for_exec>(RAJA::TypedRangeSegment<int>(0,n),[=](int k){
double temp1 = R[j][k];
double temp2 = R[i][k];
R[j][k] = c * temp1 - s * temp2;
R[i][k] = s * temp1 + c * temp2;
});
RAJA::forall<RAJA::omp_parallel_for_exec>(RAJA::TypedRangeSegment<int>(0,m),[=](int k){
double temp1 = Q[k][j];
double temp2 = Q[k][i];
Q[k][j] = c * temp1 - s * temp2;
Q[k][i] = s * temp1 + c * temp2;
});
}
}
}
vector<double> solve_linear_system_omp(vector<vector<double>> &A, vector<double> &b) {
int m = A.size();
int n = A[0].size();
vector<vector<double>> Q(m, vector<double>(m));
vector<vector<double>> R(m, vector<double>(n));
qr_decomposition(Q, R);
// Solve Q^T * b = y
vector<double> y(m, 0);
for (int i = 0; i < m; i++) {
for (int j = 0; j < m; j++) {
y[i] += Q[j][i] * b[j];
}
}
// Solve Rx = y using back substitution
vector<double> x(n, 0);
for (int i = n - 1; i >= 0; i--) {
x[i] = y[i];
for (int j = i + 1; j < n; j++) {
x[i] -= R[i][j] * x[j];
}
x[i] /= R[i][i];
}
return x;
}
public:
std::vector<double> solve(){
solve_linear_system_omp(this->A,this->b);
}
LaplaceSolverOmp(vector<vector<double>> mesh){
this->mesh=mesh;
}
};
后续计划
- 完成对RAJA的安装,从而完成对程序的RAJA改造
- 目前的算法为有限差分法,在后面一段时间中逐渐过渡到无网格法以及有限元法。
- 参考文献使用GCN对现有的分解算法进行优化