以下是统计物理第五部分相关内容
热机和第二定律
热力学第二定律
热力学第二定律是有关系统趋于平衡的过程中热量流动的方向的表述,在历史上不同人给予热力学第二定律不同的表述:
- 克劳修斯表述:不可能有这样的过程,把热量从低温物体传递到高温物体而不产生其他影响。
- 开尔文表述:不可能有这样的过程,从单一热源取出热量并使之完全变为功,而不产生其他任何影响。
- 卡诺定理描述:见下文
- 熵增表述: 在一个孤立系统中,熵总是会增加,或者在最好的情况下保持不变。
卡诺热机
开尔文表述告诉我们不可能完全把热量变成功而不产生别的影响,但是并不是不能部分把热量转换为功。
热机:一个运行于循环过程将热量转化为功的系统。
卡诺热机:运行于卡诺循环的热机
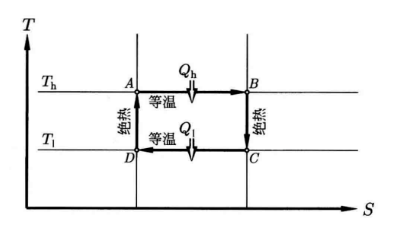
如图为卡诺循环,则卡诺热机为从$T_h$的热源吸收热量$Q_h$,输出为功$W$和热量$Q_l$
\[\begin{gathered} A\rightarrow B: Q_{h}=RT_{h}\ln\frac{V_{B}}{V_{A}} \\ B\rightarrow C: \left(\frac{T_h}{T_l}\right)=\left(\frac{V_C}{V_B}\right)^{\gamma-1} \\ C\rightarrow D: Q_{l}=-RT_{l}\ln\frac{V_{D}}{V_{C}} \\ D\rightarrow A: \left(\frac{T_l}{T_h}\right)=\left(\frac{V_A}{V_D}\right)^{\gamma-1} \end{gathered}\]则有:
\[\frac{Q_h}{Q_l}=\frac{T_h}{T_l}\]效率:效率定义为输出的功和输入热量的比值:
\[\eta = \frac{W}{Q_h}=\frac{T_h-T_l}{T_h}\]卡诺定理
卡诺定理:在工作于量给定温度热源之间的所有热机中,没有一个热机的效率高于卡诺热机
推论:工作在两个温度热源之间的所有可逆热机都有相同的效率$\eta_{\text{卡诺}}$
克劳修斯定理
考虑一个卡诺循环,定义在循环的每个点进入系统的热量为$\Delta Q_{rev}$,则
\[\sum \frac{\Delta Q_{rev}}{T}=\frac{Q_h}{T_h}-\frac{Q_l}{T_l}\]用一个积分代替求和,则有:
\[\oint\frac{\mathrm{d}Q_{rev}}T=0\]上述我们一直在考虑卡诺热机,但是对于热机来言一般不是可逆的,则
\[\oint\frac{\mathrm{d}Q_{rev}}T\leq0\]则有克劳修斯定理:对于任一闭循环,恒满足上述不等式,其中若循环是可逆的,则等号必成立
熵
熵:熵(Entropy)是一个衡量系统混乱程度或无序程度的物理量
我们由卡诺热机的克劳修斯等式可知,这表明对于路径积分:
\[\int_A^B\frac{\mathrm{d}Q_{rev}}T\]是与路径无关的,即我们可以定义这样一个态函数:
\[\mathrm{d}S=\frac{\mathrm{d}Q}{T}\]$S$即为熵,对于绝热过程,其熵不发生变化,即绝热过程是一个等熵过程
不可逆变化
熵是由可逆变化定义的,但是我们考虑这样一个过程:由一个$A\to B$的不可逆过程和一个$B \to A$的可逆过程,有:
\[\int_A^B\frac{\mathrm{d}Q}{T}+\int_B^A\frac{\mathrm{d}Q_{rev}}{T}\leqslant0\]我们可以写成:
\[\int_A^B\frac{\mathrm{d}Q}T\leqslant\int_A^B\frac{\mathrm{d}Q_{rev}}T\]则有
\[\mathrm{d}S\geq0\]根据热力学第一定律以及熵的定义,我们有:
\[\mathrm dU=T\mathrm dS-p\mathrm dV\]由于式中各量均为态函数,即与是否通过可逆过程到达无关,因此该式是普适的,则有:
\[T=\left(\frac{\partial U}{\partial S}\right)_V\\p=-\left(\frac{\partial U}{\partial V}\right)_S\]由此可以得到:
\[\frac{p}{T}=-\left( \frac{\partial U}{\partial V} \right)_S \left( \frac{\partial S}{\partial U} \right)_V=\left(\frac{\partial S}{\partial V}\right)_U\]焦耳膨胀
我们定义该不可逆过程为焦耳膨胀:$1$mol的理想气体$p_i,T_i,V_0$被限制于固体热容器的左侧,打开阀门后,气体充满整个容器$p_f,T_f,2V_0$,两容器和周围环境是热孤立的。
由于是热孤立的,即$\Delta U = 0 \to \Delta T = 0$,由理想气体状态方程,得:
\[p_f=\frac{p_i}{2}\]由于$S$为态函数,我们可以去初、末态相同的等温可逆过程计算熵变,
\[\Delta S = \int_i^f \mathrm{d}S = \int_{V_0}^{2V_0}\frac{p}{T}dV=R\ln2\]同理若我们要将气体压回左边,做的功为
\[\Delta W=-\int_{2V_0}^{V_0}p\mathrm{d}V=RT\ln2\]熵的统计学基础
我们有:
\[\frac{1}{T}=\left( \frac{\partial S}{\partial U} \right)\]根据
\[\frac{1}{k_BT}=\frac{\mathrm{d}\ln\Omega}{\mathrm{d}E}\\ S=k_B\ln\Omega\]这是宏观系统的熵的表达式
混合熵
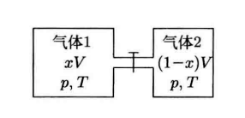
如图所示的容器,如果联通两个容器的管道上的阀门被打开,那么气体就会自发混合,导致熵的增加,这称之为混合熵。
\[\begin{aligned} \Delta S& =xNk_{B}\int_{xV}^{V}\frac{\mathrm{d}V_{1}}{V_{1}}+(1-x)Nk_{B}\int_{(1-x)V}^{V}\frac{\mathrm{d}V_{2}}{V_{2}} \\ &=-Nk_B[x\ln x+(1-x)\ln(1-x)] \end{aligned}\]这里就引入一个问题:可分辨性,如果这两种气体是相同的,在混合后就没有熵增,
麦克斯韦妖
麦克斯韦妖(Maxwell’s demon)是由苏格兰物理学家詹姆斯·克拉克·麦克斯韦(James Clerk Maxwell)在1867年提出的一个思想实验,用来探讨热力学第二定律的潜在局限性。
在这个思想实验中,麦克斯韦假设有一个微小的“妖”能够控制一个隔板上的小门,这个隔板把装有气体分子的容器分成两部分。麦克斯韦妖能够观察并分辨气体分子的速度,并选择性地让较快的分子从一侧通过小门进入另一侧,同时让较慢的分子从另一侧通过小门进入原侧。这样一来,较快的分子会逐渐集中在容器的一侧,而较慢的分子会集中在另一侧,从而导致一侧的温度升高,另一侧的温度降低,形成温差。
熵和概率
根据$S=k_B\ln\Omega$,熵可以归结于系统能够存在的不同状态数。但是每个状态可能包含大量的无法直接测量的微观态。我们假设我们设一个系统含有$N$个不同的等概率的微观态,我们有很多个宏观态,第$i$个宏观态包含$n_i$个微观态,这些宏观态被实验区分,我们有关系:
\[\sum_in_i=N\]在第$i$个微观态找到系统的概率为:
\[P_i=\frac{n_i}N\]则我们可以把系统的熵分为宏观熵和微观熵,
\[S=k_B\left(\ln N-\sum_iP_i\ln n_i\right)\]由$\ln N-\ln n_i=-\ln P_i$,则
\[S=-k_B\sum_iP_i\ln P_i\]此为熵的吉布斯表述
信息论
一个表述的信息量为:
\[Q=-k\log P\]其中$P$是表述的概率,一般$k=1$且$\log$的底数是2,此时$Q$的单位我们用比特表示。
则我们定义香农熵:
\[S=\langle Q\rangle = \sum_i Q_i P_i = -k\sum_i P_i \log P_i\]根据信息压缩原理
\[S=-k\sum_{i=1}^{2^N}P_i\log_2P_i\]